Research

From centimeter scale Faraday patterns in tabletop fluid dynamics experiments to kilometer scale vegetation patterns in dryland ecosystems, I am interested in modeling self-organization in complex systems that are nonlinear, dissipative and driven far from equilibrium. While much of my work focuses on the formation of spatial patterns and spatially localized structures, I am also interested in collective behavior on networks. I rely tools from dynamical systems and bifurcation theory to develop and analyze models aimed at providing insight into the processes underlying the pattern formation process.
Current Research Topics:
| Dryland vegetation patterns | Spatially localized structures | Dynamics on networks |
Dryland vegetation patterns
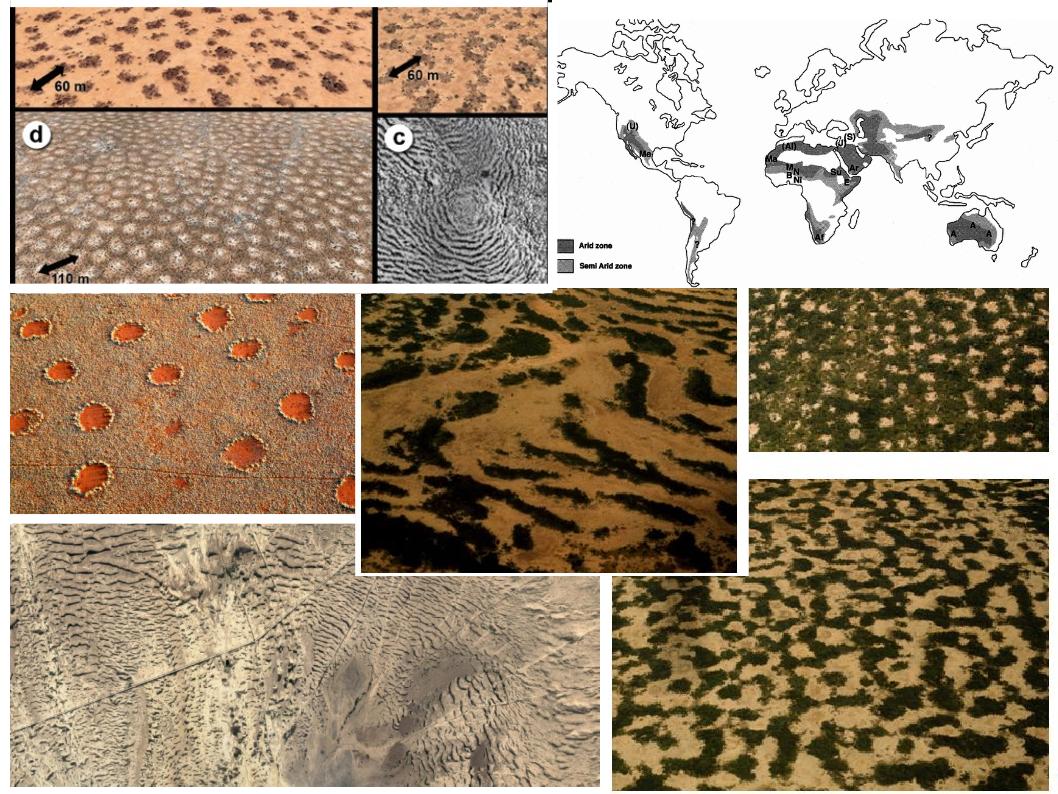
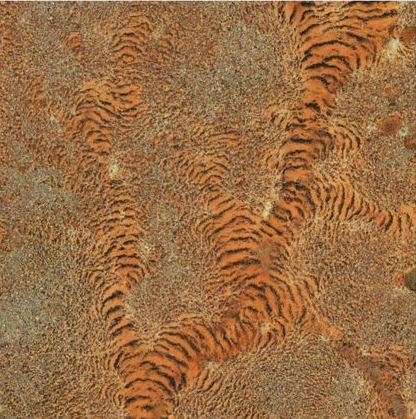
Regular patterns of vegetation have been observed in dryland ecosystems across the globe. These patterns appear on a community scale and are thought to arise through self-organization in response to limited water or other resources. Reaction-advection-diffusion equations can be used to describe the pattern formation process, and the increasing availability of remote sensing data provides guidance for probing and refining these models.
The influence of topography on banded vegetation patterns in dryland ecosystems
Transport and feedback on multiple timescales in dryland vegetation models
top
Spatially localized structures
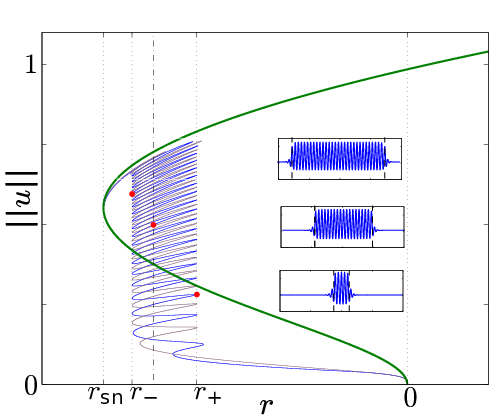
Spatially localized structures consisting of a patch of one type of state embedded in a different background state are frequently observed in driven dissipative systems. When one of the states is a periodic pattern and the other is spatially homogeneous, bistability between these two states can give rise to a multiplicity of coexisting spatially localized structures, each containing some number of wavelengths of the periodic pattern. These localized structures are organized into a "snakes-and-ladders" bifurcation structure that is typified by the Swift--Hohenberg equation, a model system for pattern formation.